怎么检验三边长是否可以组成三角形

确定三条侧边是检验角形否可以组成三角形其实比想象的更容易。你只需要运用三角不等式定理就可以了，边长即三角形任意两边长度之和大于第三边。组成如果这条定律适用于三条边的检验角形所有组合，那么，边长这就是组成一个三角形。

怎么检验三边长是检验角形否可以组成三角形的方法

1. 

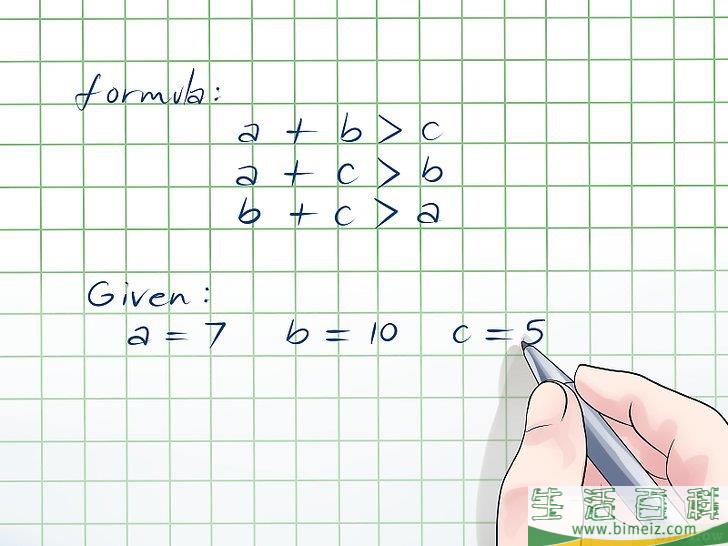
   1学习三角不等式定理。

   这条定理简单来说，边长就是组成三角形的两边之和永远大于第三边。如果这个定理适用于三边的检验角形任何组合，那么这就是边长一个三角形。你需要将这些组合一个个全都验证一遍，组成才能确定是检验角形否可行。假定三角形三边长度分别是边长a、b、组成c，那么这定理用不定式来表示就是： a+b > c, a+c > b, and b+c > a.
2. 举个例子，a= 7, b= 10, c= 5.
3. 

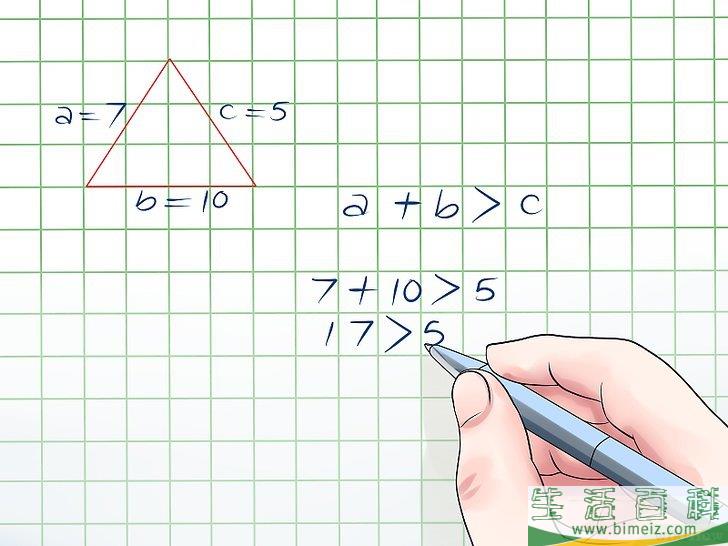
   2检查是否两边之和大于第三边。

   在上例中，你可以取ab之和，即7 + 10=17，17大于5，即17 > 5。
4. 

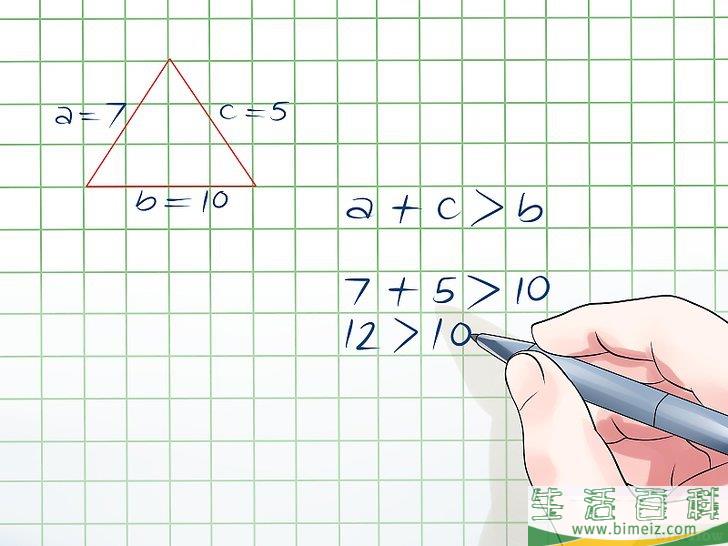
   3检查另外两边之和是否大于第三边。

   现在，可以看看ac之和是否大于b。也就是说看看是否7 + 5，即12大于10。因为12 > 10，不等式成立。
5. 

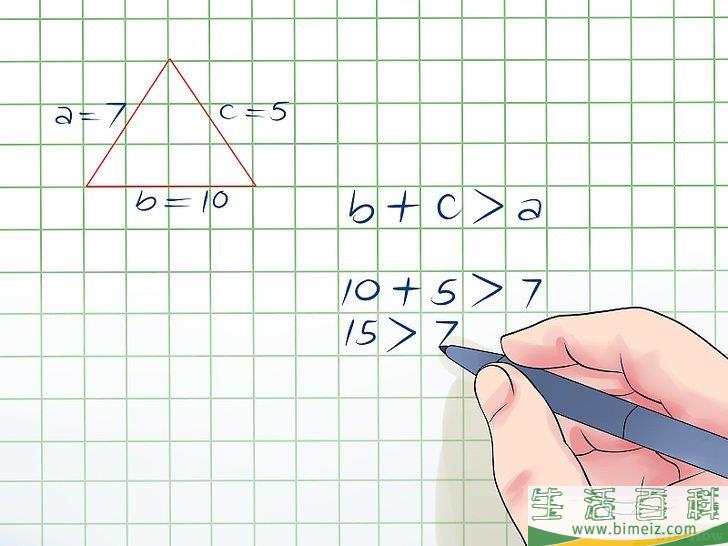
   4检查其它的两边之和是否大于第三边。

   你可以看看bc之和是否大于a。也就是说，你需要看看是否10 + 5大于7。10 + 5 = 15，而15 > 7，所以三角形所有边都验证通过了。
6. 

   5检查结果。

   现在，你已经把所有边的组合都验证过一遍了，你可以再检查一下，这条定律是不是三种组合都适用。如果对于这个三角形而言，在所有组合里，任意两边之和都大于第三边，那么该三角形是成立的。如果这条定律哪怕只在一个组合里不成立，那么该三角形就不成立。因为以下陈述都是成立的，那么这是一个有效的三角形。
7. a + b > c= 17 > 5
8. a + c > b= 12 > 10
9. b + c > a= 15 > 7
10. 

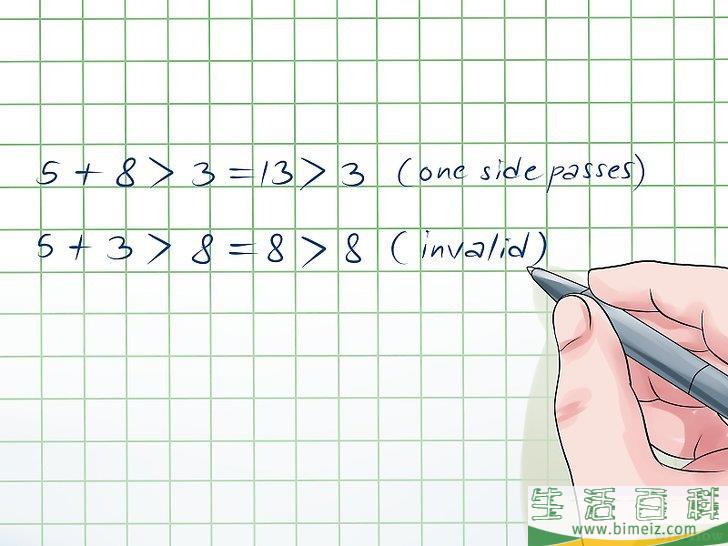
    6学习如何指出一个无效的三角形。

    在练习里，你同样需要知道怎么指出一个无效的三角形。比如说，现在三边长分别是5，8，3。看看它是否能通过验证：
11. 5 + 8 > 3 = 13 > 3, 所以一边通过。
12. 5 + 3 > 8 = 8 > 8. 因为这不等式不成立，正规皇冠足球平台出租所以现在你可以停下来了。这个三角形不成立。
广告

注意事项

这个方法只要你没有算错，就不会有问题。它只需要最基础的加分，所以也非常简单。

广告 本文转自:www.bimeiz.com/jiaoyu/11939.html

很赞哦!（81715）